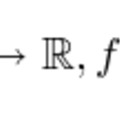Egy forgó merev test minden nemnulla sebességű pontjának pillatatról pillanatra változik a sebességvektora. Mégis van értelme "változatlan forgás"-ról beszélni, olyan értelemben, hogy egy egyenletesen forgó merev testnek a tér adott pontján éppen ott lévő pontjának a sebessége időben állandó. Vagyis egy egyenletesen forgó merev test mozgása időben állandó sebességmezővel írható le.
Ez a megállapítás természetesen a merev test forgás nélküli egyenletes transzlációjára is alkalmazható, de ott persze maguknak a tömegpontoknak is konstans a sebességük. Ellenben egy változó keresztmetszetű csőben stacionáriusan áramló összenyomhatatlan folyadék esetén ismét már csak a sebességmező az, ami állandó, a folyadék egyes pontjainak a sebessége már nem. A fenti példák arra utalnak, hogy a kiterjedt testek mozgásának leírására bizonyos szempontból praktikusabb módszer lehet a test sebességmezejének a jellemzése, mint annak a vizsgálata, hogy a test egyes pontjai hogyan mozognak.
Maradjunk a forgó merev testnél. A test forgását a test sebességmezejével szeretnénk jellemezni , tudván, hogy a test egy lehetséges helyzetét minden esetben egy forgatással - vagyis az SO(3) csoport egy elemével - lehet egy másik lehetséges helyzetébe vinni.
Tegyük fel, hogy adva van a test egy önkényesen kiválasztott helyzete, és ebben a helyzetben minden p pontjának ismerjük az R3 térbeli r0(p) helyzetvektorát. Tetszőleges t pillanatban a test tetszőleges pontjának a helyvektora egy g(t) ∈ SO(3) csoportelemmel származtatható az általunk lefixált helyzetéből: r(p,t) = g(t)(r0(p)), vagy magának a p pontnak a jelölését elhagyva: r(t)= g(t)(r0) (a továbbiakban a test pontjait azonosítjuk kiválasztott helyzetbeli helyvektorukkal). Tehát adott t pillanatban a test összes pontjának a pillanatnyi helyzete ugyanazzal az egyetlen SO(3)-beli g(t) elemmel jellemezhető. Ez az összes t pillanatra vonatkoztatva azt jelenti, hogy a merev test adott forgása esetén a különböző pontja által R3-ban leírt összes különböző r(t) görbét egyetlen SO(3)-beli g(t) görbe határozza meg. Sőt. Mint említettük, minket most a test sebességmezeje érdekel, és nem az hogy test egyes pontjai hogyan mozognak. Más szóval (a sebességmezőt integrálva) az egyes pontok trajektóriáinak a halmaza, függetlenül attól, hogy a test melyik pontjához melyik trajektória tartozik. Tetszőleges h ∈ SO(3) esetén a g(t) és a g(t)h SO(3)-beli görbe ugyanazt a forgást írja le, csak egy kiszemelt trajektória az első esetben az r0, míg a második esetben a h-1(r0) ponthoz tartozik.
Mi most a pontok sebességeit, vagyis ezeknek az R3 -beli görbéknek az érintőit szeretnénk kapcsolatba hozni SO(3) érintővektoraival, vagyis az SO(3)-beli görbék érintőivel.
Mivel minden egyes r helyvektor meghatároz egy Fr : SO(3) → R3 : g → Fr(g): = g(r) leképzést, ennek az érintőleképezése a megfelelő érintőterek között határoz meg egy DFr leképezést: DFr : TSO(3) → TR3 : w → DFr(w). A definícióból közvetlenül adódik, hogy tetszőleges i ∈ SO(3) elemre Fr(g) = g(r) = g(i-1i(r)) = (gi-1)(i(r)) = Fi(r)(gi-1). Ha az i-1 elem SO(3)-on való jobboldali csoporthatását, vagyis az SO(3) → SO(3): g → gi-1 hozzárendelést Ri-1 -gyel jelöljük, akkor az összefüggésünket Fr(g) = Fi(r)(Ri-1(g)) alakban írhatjuk. Az összefüggés természetesen tetszőleges g(t) görbe összes pontjára is érvényes: Fr(g(t)) = Fi(r)(Ri-1(g(t))), így e görbék érintőire is:
DFr(w) = DFi(r)(DRi-1(w)) (1)
Az R3 x TSO(3) -> TR3 : (r, w) -> DFr(w) hozzárendelést felfoghatjuk úgy is, hogy SO(3) minden w érintővektora meghatároz egy Gw: R3 -> TR3 : r -> DFr(w) leképezést. Tekintve, hogy SO(3) elemei R3 lineáris transzformációi, TR3 pedig azonosítható R3-mal, valamint a deriválás is lineáris, ezért Gw egy R3 -> R3 lineáris függvénynek tekinthető.
Ez már majdnem a forgó test sebességtere, de nem teljesen. Ha a w érintővektor a h ∈ SO(3) pont felett van (vagyis, ha w ∈ ThSO(3)), akkor Gw(r) a következő leképezés. Tetszőleges h-n átmenő és ebben a pontban w érintőjű g(t) SO(3)-beli görbét véve Gw(r) a g(t)(r) R3-beli görbe h(r) pontbeli érintője. Nekünk viszont egy olyan hozzárendelés kell, amelyik nem az r, hanem a h(r) ponthoz rendeli hozzá ezt az érintővektort. A keresett sebességmező tehát az R3 -> TR3 : r -> Gw(h-1(r)) leképezés. Az (1) összefüggés és Gw definíciója szerint ez
r -> DFr(DRh-1(w)) (2)
alakba is írható.
Az itt szereplő TSO(3) → TeSO(3)) (= so(3)) : w → DRh-1(w) lineáris leképezés tetszőleges h ∈ SO(3) esetén minden h feletti érintővektorhoz az SO(3) csoport e egységeleme feletti vektort rendel hozzá, mégpedig úgy, hogy ha egy h-n átmenő, h-ban w érintőjű SO(3)-beli görbét az Rh-1 csoporthatással egy e-n átmenő görbébe viszünk, akkor DRh-1(w) ennek az utóbbi görbének az érintője az e pontban.
A DRh-1(w) lineáris leképezést (más szóval, ezt a Lie-algebra értékű 1-formát) nevezik Maurer-Cartan formának. Az itt bevezetett Maurer-Cartan forma különleges tulajdonsága, hogy a jobb-invariáns vektormezőkön konstans az értéke. Jobb-invariánsnak akkor nevezünk egy X vektormező, ha tetszőleges g, h ∈ SO(3) esetén DRh(X(g))= X(gh). (Természetesen, ha a jobboldali csoporthatás helyett baloldalit veszünk, akkor a balinvariáns Maurer-Cartan formához jutunk).
De térjünk vissza a merev testünkhöz. A (2) összefüggés szerint a merev test sebességmezeje r → v(r) = DFr(u) alakú, ahol u ∈ TeSO(3) , vagyis u az so(3) Lie-algebra eleme. Ez azt jelenti, hogy valamely e-n átmenő t → g(t) SO(3)-beli görbével v(r) = (d/dt)(Fr(g(t))) = (d/dt)(g(t)r), ahol a deriválás abban a t pontban értendő, amelyre g(t) = e. Az általánosság megszorítása nélkül feltehetjük, hogy g(0) = e. Lévén, hogy SO(3) elemei izometriák, tetszőleges t esetén ||g(t)r||2 = ||g(0)r||2, vagyis 0 = (d/dt)|t=0(||g(t)r||2 ) = (d/dt)|t=0<g(t)r,g(t)r)> = 2<(d/dt)|t=0g(t)r, g(0)r)> = 2 <v(r),r> , ahol <> a skalárszorzatot jelöli, és az érintővektorokat azonosítottuk a vektorokkal (ld. 12. Affin terek ) Az r → v(r) = DFr(u) leképezés tehát egy antiszimmetrikus lineáris leképezés, hiszen <v(r), s> + <v(s), r> =<v(r), s> + <v(s), r> +<v(r), r> + <v(s), s> = <v(r), s + r> + <v(s), r + s> = <v(r+s),r+s> = 0. A 3-dimenziós euklideszi tér önmagára történő antiszimmetrikus lineáris leképezései 3-dimenziós vektorteret alkotnak, tehát izomorfia létesíthető közöttük és R3 elemei között. Az ilyen módon az r → v(r) = DFr(u) sebességmezőhöz rendelt ωu vektort nevezzük a forgó merev test szögsebesség-vektorának. Ezzel az ωu vektorral felírva DFr(u) = ωu x r, ahol x a szokásos vektoriális szorzatot jelöli.
Mátrix-reprezentáció
Ha SO(3) elemeit a szokásos módon 3x3-as 1 determinánsú ortogonális mátrixokkal reprezentáljuk, és a továbbiakban külön jelölés helyett SO(3) tetszőleges g elemén egy ilyen mátrixot értünk akkor Fr(g) = gr. TSO(3) elemei olyan mátrixok, amelyek t->g(t) mátrix-értékű függvények deriváltjai. A deriválás mátrixelemenként végezhető el.
A Maurer-Cartan forma ebben a reprezentációban a w → wh-1, ahol w valamely t → g(t) 1 determinánsú ortogonális mátrix értékű függvény deriváltja abban a t pontban, amelyben g(t) = h. Mint láttuk, az eredmény egy antiszimmetrikus transzformáció mátrixa lesz, vagyis egy antiszimmetrikus mátrix. Ennek a mátrixnak a Hodge-duálisa a szögsebesség vektor.