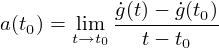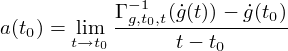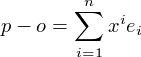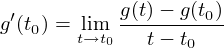Az érintőnyalábokon megadott konnexiók értelme, hogy pótolják azt a hiányosságot, amellyel az affin terek eleve rendelkeznek: a vektorok eltolhatóságát, illetve a különböző pontokhoz tartozó érintővektorok összehasonlítását. Ha például most a téridőre, mint egy 4-dimenziós sokaságra gondolunk, akkor a téridőbeli görbék a pontszerű részecskék világvonalai. A részecskék sebessége minden pontban a sokaság egy érintővektora. A gyorsulásukat viszont csak akkor tudjuk megmondani, ha valahogy össze tudjuk hasonlítani a különböző pontbeli sebességeiket. Kicsit formálisabban elmondva ugyanezt: Ha a részecskénk világvonala mondjuk a g:[0,1] → M görbe (ahol M a 4-dimenziós téridő, mint differenciálható sokaság), akkor ennek a részecskének a t0 pontbeli sebessége a görbének a g(t0)- beli érintővektora a
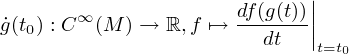
(1)
deriváció.
A részecske gyorsulása
(2)
lenne, ha lenne értelme a g.(t) - g.(t0) különbségnek. De nincs, mivel g.(t) a Tg(t)M vektortérnek, g.(t0) pedig a Tg(t0)M -nek az eleme, és különböző vektorterek elemei közt nincs értelmezve a kivonás művelete.
Ha azonban TM-en adva van egy konnexió, az azt jelenti, hogy értelmezve van tetszőleges v ∈ Tg(t0) vektornak a g görbe mentén a Tg(t)M -be történő párhuzamos eltolása. Ha a konnexiónk lineáris, akkor ez egy Γg,t0,t : Tg(t0)M → Tg(t)M lineáris leképezés. Ha még nem elfajuló is ez a leképezés, akkor létezik a Γg,t0,t-1 : Tg(t) → Tg(t0)M inverze is.
Ezzel már tudjuk definiálni a gyorsulást:
(3)
Tehát a differenciahányados számlálóját úgy számoljuk, hogy a g(t) beli sebességet a g görbe mentén párhuzamosan visszatoljuk Tg(t0) be, ahol már ki tudjuk vonni belőle a g(t0) -beli sebességet. Látható, hogy a konnexió linearitására azért van szükség, hogy az így definiált gyorsulás a sebességnek ugyanúgy lineáris függvénye legyen, mint ahogy azt megszoktuk.
Mondanom sem kell, hogy ez abszolút gyorsulás, hiszen semmiféle koordinátákat nem használtunk a definiálásához. A konnexiót pedig Newton I. törvénye biztosítja számunkra - szintén megfigyelőfüggetlen módon. Az majd a következő kérdés lesz, hogy ilyen-olyan koordinátákkal hogy lehet ezt kiszámolni.
De egyelőre nézzük meg ezt a dolgot az affin terek esetében.
Egy nem üres M halmazt, a V vektortér feletti affin térnek nevezünk ha M elemei között értelmezve van a kivonás művelete, vagyis adva van egy M x M → V, (x,y) → x - y leképezés amelyre
- tetszőleges o ∈ M esetén az Oo: M → V , x → x - o leképezés bijektív
- (x-y) + (y-z) + (z-x) = 0.
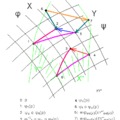
Az n-dimenziós affin tereket sima sokaságoknak is tekinthetjük, ha atlasznak az affin koordinátákat tekintjük, vagyis V tetszőleges {ei} bázisához és M tetszőleges o pontjához azt a Φ: M → Rn, p → {x1,...xn} térképet választjuk, amelyre
. (4)
A topológiát az a feltétel egyértelműen definiálja M-en, hogy ezek a térképek homeomorfizmusok legyenek (ez az affin terek ú.n. természetes topológiája).
A fenti módon sima sokaságnak tekintett affin terekben egy g görbe érintővektorát egyrészt ugyanúgy definiálhatjuk, mint bármilyen sima sokaság esetén (vagyis az (1) képlettel), másrészt definiálhatjuk a
képlettel is, hiszen affin terek esetén a kivonásnak van értelme a számlálóban, és a valós számmal való osztásnak is.
Az így definiált g'(t) a V vektortér eleme, nem pedig egy deriváció, mint g.(t).
Az, hogy g'(t) t-től függetlenül ugyanannak a V vektortérnek az eleme, számunkra örvendetes, mert ha az így definiált érintővektort tekintjük sebességnek, akkor a használhatatlan (2) képletben g. helyett g'-t írva az máris használhatóvá válik:
![]()
(5)
A kétféle érintővektor közti kapcsolat:
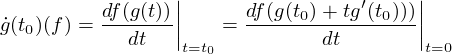
.
A kétféle érintővektor azonosíthatósága (3)-ra pillantva azt sugallja, hogy az affin tér struktúrája meghatározza az érintőnyalábjának egy természetes konnexióját.