Az előző bejegyzésben láttuk, hogy az LXY Lie-deriválás értéke a p pontban egy olyan vektor, ami az X vektormezőnek (vagyis a rátóti legények sebességmezejének) a p ponton áthaladó φp integrálgörbéje mentén összehasonlítja az Y (a létra szabad ága irányába mutató) vektormezőnek ahhoz az Y' vektormezőhöz viszonyított változását, ami az Yp vektornak a φ folyammal történő pushforwardjaiból áll (ez a létra fogott ága irányába mutató vektormező). Pusztán az Yp pont és a φp görbe még nem határozzák meg az Y' vektormezőnek a φp görbén felvett értékeit. A pushforwardhoz szükségünk van az X vektormező értékére a p pont egy teljes környezetében (hiszen ha a létra zsanérját fogó legénynél gyorsabb a mellette jobbra haladó, akkor a létra balra ferdül, ha pedig lassabb, akkor jobbra).
Ha most az Y' vektormező helyett egy olyan Y'' vektormezőt veszünk, ami az Yp pontnak a φ görbe mentén való párhuzamos eltoltjaiból áll, akkor az LXY Lie-derivált helyett a ∇XY kovariáns deriválthoz jutunk. Az Y vektormezőnek az X vektormező mentén vett kovariáns deriváltjának p pontbeli (∇X Y)p értéke a Lie-deriválttal szemben nem függ az X vektormezőnek a p ponton kívüli értékeitől, viszont szükség van hozzá a párhuzamos eltolást meghatározó konnexióra. Ez olyasmi, mint ha az előző bejegyzésbeli rátóti legények helyett egyetlen legény vinné a létrát, és valaki (vagy pl. egy iránytű) előírná neki, hogy milyen irányban tartsa a létra fogott ágát menet közben.
Láttuk másrészről azt is, hogy a Lie-deriválás a létra kinyílási sebességén kívül azt méri, hogy két különböző folyam mentén egymás után azonos ideig haladva mennyire különbözik a végső helyzetünk, ha először az egyik, majd a másik folyam mentén haladunk attól, ha ezt fordított sorrendben tesszük. Ez az előző bejegyzés végén szereplő
f( ψs º φt(p)) - f(φt º ψs(p))
képlet jelentése t = s esetén. A Lie-derivált ennek a különbségnek és t2-nek határértéke a t → 0 esetben:
(LXY)f = limt→0(1/t2)[ f( ψt º φt(p)) - f(φt º ψt(p))]
ami persze azonos az általunk eredetileg felírt
limt,s→0(1/st)[ f( ψs º φt(p)) - f(φt º ψs(p))]
határértékkel, ha ez utóbbi létezik.
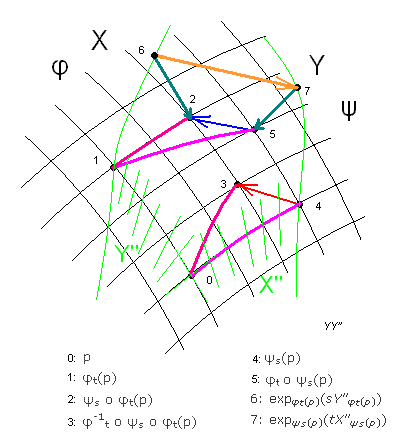
Az LXY (= [X, Y]) Lie-deriváltat az ábrán az 5 → 2 kék vektor, az
(∇X Y)f = limt,s→0(1/st)[ f( ψs º φt(p)) - f(expφt(p)(sY''φt(p))]
kovariáns deriváltat a 6 → 2, az
(∇Y X)f = limt,s→0(1/st)[ f(φt º ψs(p)) - f(expψs(p)(tX''ψs(p)))]
kovariáns deriváltat pedig a 7 → 5 sötétzöld vektorok szemléltetik.
Az ábrán szereplő 6 → 7 (barna) vektor azt a különbséget szemlélteti, ami a p pontból kiinduló X, majd Y irányú geodetikusok mentén t illetve s ideig való, illetve a fordított sorrendű haladás eredményének a különbsége. Az X illetve az Y irány a p-től különböző pontokban úgy értendő, hogy ezek az Xp illetve az Yp vektornak a görbe mentén való párhuzamos eltoltjai (és nem az X és az Y vektormező ottani értéke!). Tehát az X és Y vektormezőnek a p pontbeli Xp és Yp értékeiből a konnexió már meghatározza ennek a különbségnek a határértékét. És persze a határértéket az sem befolyásolja, ha X és Y érintőjű geodetikus helyett egyéb X ill. Y irányú görbét veszünk (mint ahogy jelen esetben is φt (p)-t ill. ψs(p)-t használtunk p-ből induló szakaszokként).
A 6 → 7 vektor a fentiek alapján és az ábráról leolvashatóan a
(Xp, Yp) → (∇X Y)p - (∇Y X)p - [X, Y]p
hozzárendelést jelenti. Ez a hozzárendelés lineáris, tehát egy (1,2)-típusú tenzormező. A neve: a konnexió torzió tenzora.