Folytassuk rombolásunkat! Paul Dirac derékszíját már sikerült tönkretennünk a vastag gombostűkkel, most egy gumilabdát vágjunk félbe. Olyat keressünk, amit amúgy is két félgömbből ragasztottak össze, mert ezen szépen látszik a ragasztás nyoma, mint valami egyenlítő: itt vágjuk szét. Ha nem túl erős a labda (vagy inkább: ha a képzelőerőnk kellően erős), akkor ezt a fél-labdát szépen egy koronggá tudjuk kisimítani.
A korong nem más, mint egy 2-dimenziós tömör gömb. Nevezzük D2-nek! A korong határa egy kör, vagyis egy 1-dimenziós gömbhéj (S1). Maga a gumilabda pedig egy 3-dimenziós térben lévő 2-dimenziós gömbhéj (S2).
Most lépjünk egy dimenzióval feljebb! Korong (vagyis a 2-dimenziós tömör gömb, D2) helyett vegyünk egy rendes, 3-dimenziós tömör gömböt (D3). Ezt nyilván egy 4-dimenziós térbeli gumilabda (S3) kettévágásával és kisimításával tudjuk létrehozni.
A 3-dimenziós tömör gömbbel az előző bejegyzésben úgy tudtuk a 3-dimenziós forgatások topológiáját leírni, hogy a felszíni, egymással átellenes pontjait azonosítottuk. Egy dimenzióval lejjebb ez a - kisimított, vagy kisimítatlan - fél gumilabda egyenlítőjének az átellenes pontjainak egymással történő azonosítását jelenti. Ez így nem elég szép. Ragasszuk csak vissza a helyére a gumilabda levágott déli félgömbét is, és azonosítsuk a déli félgömb minden pontját az északi félgömbnek a vele átellenes pontjával. Így a labda minden pontja azonos a vele szemben lévővel. Az ilyen ekvivalenciarelációval ellátott S2-nek ugyanaz a topológiája, mint a fél gumilabdáé (2-dimenziós tömör gömbé, azaz D2-é) ha annak a határpontjain (az egyenlítőn) definiáljuk ezt az ekvivalenciarelációt. Akármelyik reprezentációt vesszük, amit a megfelelő hányadosterek leírnak, az RP2, vagyis a valós projektív sík.
A 3-dimenziós forgatások topológiája pedig RP3 -mal (a valós projektív térrel) azonos, ami az előzők 1-dimenzióval feljebb való megismétlésével azt jelenti, hogy nem csak D3/{szemben lévő határpontok ekvivalenciája}, hanem S3/{szemben lévő pontok ekvivalenciája}-ként is előáll.
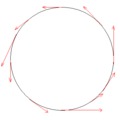
Mivel S3 a 4-dimenzós térben lévő gömbhéjat jelenti, ő magát nem tudjuk szemléletesen elképzelni, csak a 3-dimenziós térbeli S2 metszeteit. Az egy dimenzióval lejjebbi gumilabda esetén egy ilyen metszet a gumilabdának egy délköre. A különböző délkörök különböző sugarú körök (1-dimenziós gömbhéjak). Ennek megfelelően S3-at úgy lehet elképzelni, mint ami hasonlóan van összerakva a D3 belsejéből kiszedett különböző sugarú gömbhéjakból, mint ahogy a gumilabda "van összerakva" a különböző sugarú délköreiből.
A forgatásokra visszatérve S3 tehát úgy reprezentálja a forgatásokat, hogy egy adott α esetén az α szögű forgatások S3 -nak egy α sugarú metszetében vannak, vagyis egy α sugarú 3-dimenziós gömbhéjon, ugyanúgy, mint ahogy az a D3-mal történő reprezentálás esetében is volt.