Newton törvényeitől a Higgs-bozonig

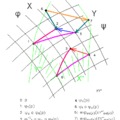
Annak ellenére, hogy egy nyaláb trivializációja lényegében véve önkényes, egy ilyen önkényes trivializáció átmeneti függvényeit megvizsgálva meg tudjuk mondani, hogy a nyaláb triviális-e, vagy sem.

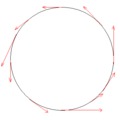
Példaként nézzük a nemtriviális Möbius-szalagot illetve a triviális hengerpalástot. Rakjuk össze a hengerpalástot az előző bejegyzésben írt módon, három papírcsíkból. Ekkor a 3 papírcsíknak 3 átfedése van. A 4. bejegyzés jelöléseit használva a papírcsíkok rendre az U_i × [-1,1] halmazok (i ∈ {1,2,3} ). Az átmeneti függvények 1-gyel, ill. -1-gyel történő szorzások. Az első módon leírt összerakásban: g₁₂ = g₂₃ = g₃₁ = 1. A második esetben, vagyis amikor a második papírcsíkot megfordítottuk, az átmeneti függvények: g₁₂ = g₂₃ = -1,  g₃₁ = 1. Az átmeneti függvények mindkét esetben faktorizálhatók g_ij = λ_i λ_j alakban: az első esetben λ₁ = λ₂ = λ₃ = 1 , a másodikban pedig λ₁ = λ₃ = 1,  λ₂ = -1 értékekkel.

A Möbius-szalag esetén a papírcsíkokat úgy kell összeragasztani, hogy valamelyik csíknak az egyik felét ragasztjuk fordítva a következőhöz, mondjuk a harmadik szalagot az elsőhöz: g₁₂ = g₂₃ = 1, g₃₁ = -1. Ha ebben az összeállításban a második szalagot megfordítjuk, az átmeneti függvények ezek lesznek: g₁₂ = g₂₃ = g₃₁ = -1. Ezek a g_ij függvények láthatóan nem faktorizálhatók  λ_i λ_j  alakban, hiszen g_ij = λ_i λ_j esetén  g₁₂ g₂₃ g₃₁ = (λ₁λ₂)(λ₂λ₃)(λ₃λ₁) = λ₁²  λ₂² λ₃² = 1 lenne és nem -1.

És ez általában is igaz! Egy fibrált nyaláb pontosan akkor triviális, ha egy trivializéciójához tartozó g_ij átmeneti függvények  λ_i λ_j alakban faktorizálhatók. Ez egyúttal persze azt is jelenti, hogy egy nyalábnak vagy az összes trivializációja faktorizálható ámeneti függvényekkel rendelkezik, vagy egyik sem.