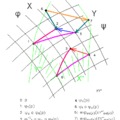
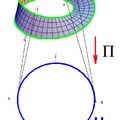
Legyen adva egy p pont egy fibrált nyaláb teljes terében, valamint a nyalábon legyen adva egy konnexió, tehát a nyaláb teljes terének minden egyes e pontjában az e feletti TeE érintőtérnek egy VeE ⊕ HeE = TeE felbontása, ahol VeE = ker(dΠe) = Te(Π−1(Π(e)), vagyis TeE vertikális altere.
Definíció. A fibrált nyaláb bázisterében haladó g(t) görbének a p pontba való felemelése alatt a nyaláb teljes terében haladó olyan h(t) görbét értünk, amelyre h(0) = p és Π(h(t)) = g(t). A felemelést horizontálisnak nevezzük, ha a h(t) görbe érintője minden pontban horizontális, vagyis Hh(t)E eleme.
Állítás. A horizontális felemelés egyértelmű.
Bizonyítás. A nyalábunk legyen (B, E, Π, V) (a nyaláb bázisterét most nem az ebben a blogban eddig szokásos T-vel, hanem az általában szokásos B-vel jelölöm), és legyen adva rajta egy konnexió. Legyen a görbénk g: [0,1] → B, h: [0,1] → E pedig legyen a g görbe egy horizontális felemeltje.
Vegyünk a [0,1] intervallumban egy tetszőleges t számot. Mivel h a g felemelése ezért Π(h(t)) = g(t), így dΠ(h.(t)) = g.(t), ahol h.(t) ill. g.(t) a g ill. h görbe g(t)-beli ill. h(t)-beli érintővektorai. Másrészt, ha v és w a (Π−1(g(t)) halmaz tetszőleges e pontja feletti TeE érintőtér olyan vektorai, amelyekre dΠ(v) = dΠ(w), akkor a dΠ érintőleképezés linearitása miatt ez azt jelenti, hogy dΠ(v- w) = 0, vagyis v és w különbsége egy vertikális vektor (tehát VeE eleme). Így a h.(t) vektorra kirótt másik feltétel, vagyis, hogy a vertikális komponensének nullának kell lennie, tetszőleges e ∈ Π−1(im g) pontban már egyértelműen meghatározza h.(t)-t. Ezek szerint a h-ra magadott két feltétel a Π−1(im g) halmazon meghatároz egy vektormezőt, amelynek h(t) egy integrálgörbéje. A Picard-Lindelöf tétel szerint a Π−1(im g) halmaz tetszőleges pontján át pontosan egy ilyen integrálgörbe halad át, tehát a g görbének adott pontba való felemelése egyértelmű.