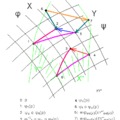
Állítás. Ha q = (cos(φ/2) , usin(φ/2)), akkor
q(0,v)q-1 = (0, v'),
ahol v' a v vektor u körüli φ szöggel való elforgatottja.
Bizonyítás.
Tekintve, hogy a (0,v) -> q(0,v)q-1 hozzárendelés v-ben lineáris, az állítás az alábbi két állítással ekvivalens:
q(0,v)q-1 = (0,v), ha v = u
q(0,v)q-1 = (0, vcosφ + (u x v)sinφ ), ha v merőleges u-ra , vagyis, uv =0 és u x v x u = v
Ezek az összefüggések pedig a
q(0,v)q-1 = (cos(φ/2) , usin(φ/2)) (0,v) (cos(φ/2) , -usin(φ/2))
szorzás elvégzésével egyszerűen láthatóan teljesülnek.
Az első szorzás eredménye:
(cos(φ/2) , usin(φ/2)) (0,v) = (-uvsin(φ/2), vcos(φ/2) + sin(φ/2) u x v )
A másodiké:
(-uvsin(φ/2), vcos(φ/2) + sin(φ/2) u x v ) (cos(φ/2) , -usin(φ/2)) =
= (-uvsin(φ/2)cos(φ/2) + vucos(φ/2)sin(φ/2) + sin(φ/2) (u x v) usin(φ/2),
(uv)sin2(φ/2)u + vcos2(φ/2) + sin(φ/2)cos(φ/2) u x v - (vcos(φ/2) + sin(φ/2) u x v) x usin(φ/2) =
= (0, (uv)sin2(φ/2)u + vcos2(φ/2) + 2sin(φ/2)cos(φ/2) u x v - sin2(φ/2) (u x v) x u ).
Ha v=u, akkor ebből
q(0,v)q-1 = (0, v),
ha pedig vu=0, akkor
q(0,v)q-1 = (0, v(cos2(φ/2) -sin2(φ/2)) + 2sin(φ/2)cos(φ/2) u x v ) =
= (0, vcosφ + (u x v)sinφ).