Merthogy nemcsak libát loptak szegények, hanem létrát is vittek az erdőben. Keresztben.
A legények egy folyamot képeznek a felületen, a létra pedig egy vektor, amit a folyam tol előre (ld. pushforward). A legények folyama egy φ : (R x M) → M : (t, p) → φt(p) leképezés. A t = 0 pillanatban a p pontban tartózkodó legény a t pillanatban a φt(p) pontban van. Most képzeljük el, hogy a létra, amit visznek, egy kétágú létra, ami útközben kinyílik. A kinyíló szabad ág (csakúgy, mint a fogott ág) a létra zsanérjából mutat valamerre, vagyis ő a zsanér által leírt görbe minden pontjában egy ottani érintővektor. Legyen Y egy olyan vektormező a felületen, amely ezen a görbén azonos kinyílt ág által meghatározott vektorral. Tegyük fel, hogy a létra éppen zárva van, amikor a zsanér éppen a felület p pontjában tartózkodik. Tartozzék e a pillanat a t = 0 időponthoz. Ettől eltérő t pillanatban a létra szabad ága a φt(p) pont feletti Yφt(p) vektor, a fogott ága pedig a φt*(Yp) vektor, ahol φt* a φt leképezés érintőleképezése (pushforwardja).
A kinyíló ághoz tartozó Y vektormezőnek a legények X sebességmezeje szerinti Lie-deriváltja a létra fogott ága nemzsanéros végéből a kinyíló szabad ág nemzsanéros végébe mutató vektor idő szerinti deriváltja:
LXY = limt→0(1/t)[Yφt(p)- φt*(Yp)],
Sajnos ez a definíció csak görbületmentes felületen jó, ahol a különböző pontok feletti érintővektorok ugyanannak a vektortérnek az elemei.(1) Az általános esetben a Lie-deriváltat egy picit másképp kell definiálnunk azért, hogy az itt leírt deriválandó időfüggő vektor minden t pillanatban a p pont feletti vektortérnek legyen eleme. Azt csináljuk, hogy a fenti összefüggésben mindkét tagot φt* inverzével visszatoljuk a p pontba:
LXY = limt→0(1/t)[φ-1t*(Y φt(p)) - Yp] = (d/dt)|t=0[φ- 1t*(Yφt(p))]
Nézzük meg, hogy hat ez a vektor, mint deriváció egy az M sokaságon megadott valós értékű függvényre!
(LXYf)(p) = limt→0(1/t)[(φ-1t*(Y φt(p))f)(p) - Ypf (p)]
A pushforward definíciója szerint
[φ-1t*(Yφt(p))f](p) =[Yφt(p) (φ-1t*(f )](φt(p)) = [Y(f º φ- 1t)](φt(p))
Ezzel
(LXYf)(p) = limt→0(1/t)[([Y(f º φ- 1t)](φt(p)) - Yf (p)] (*)
A fenti kéttagú kifejezés második tagja:
Yf(p) = d/ds|s=0(f(ψs(p)) = lims→0(1/s)[f(ψs(p)) - f(p)],
ahol ψ az Y vektormező által meghatározott folyam. Az első tag:
[Y(f º φ- 1t)](φt(p)) = d/ds|s=0((f º φ- 1t(ψs(φt(p)))
= lims→0(1/s)[f º φ-1t(ψs (φt(p))) - f º φ-1t(φt(p))]
= lims→0(1/s)[f º φ-1t º ψs º φt (p) - f(p)]
Így tehát
LXYf = limt,s→0(1/st)[ f(φ-1t º ψs º φt(p)) - f(p) - f(ψs(p)) + f(p)]
= limt,s→0(1/st)[ f(φ-1t º ψs º φt(p)) - f(ψs(p))]
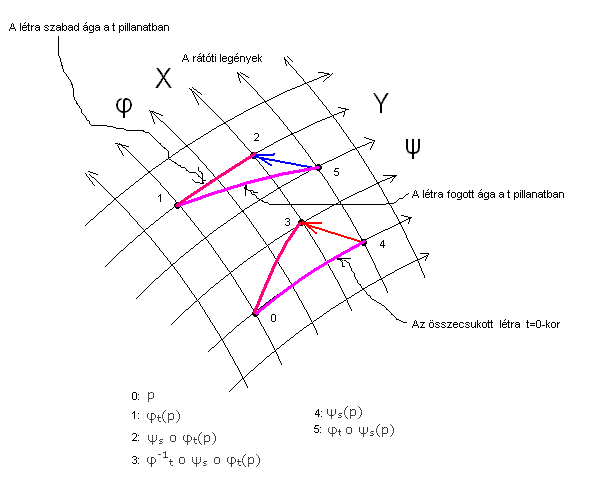
Az ábrán szereplő sorszámokkal:
LXYf = limt,s→0(1/st)[f(3) - f(4)],
amit az ábrán a 4 → 3 piros vektor szemléltet.
Igenám, de mi eredetileg az 5 → 2 kék vektorra lettünk volna kíváncsiak, hiszen ez az a vektor, ami a létra fogott szára végéből a szabad szár végébe mutat. Vagyis mi a
limt,s→0(1/st)[f(2) - f(5)] = limt,s→0(1/st)[ f( ψs º φt(p)) - f(φt º ψs(p))]
eredményt szerettük volna kapni, ami könnyen láthatóan a jól ismert [X,Y]f = X(Yf)-Y(Xf) kommutátorral azonos. Elrontottunk volna valamit?
Nem! Bármily hihetetlen is, ez a két kifejezés egyenlő egymással!
(1) Mivel most lokális fogalmat definiálunk, az esetleges többszörösen összefüggés globális tulajdonságnak itt nincs szerepe, tehát most nyugodtan gondolhatunk parallelizálható sokaságra, amikor görbületmenteset mondunk.