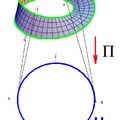
A szelés a folytonos függvény fogalmának általánosítása Descartes-szorzatokról fibrált nyalábokra.
A függvény - mint tudjuk - két halmaz Descartes-szorzatának egy részhalmaza. Például a f(x) = 2x függvény a Gf = {(x,2x)|x ∈ R} halmaz. Általában pedig egy f: H → K függvény az E = H × K halmaznak olyan Gf részhalmaza, hogy H tetszőleges x eleméhez pontosan egy olyan e eleme van Gf -nek, hogy proj1(e) = x.
Ha a szelés fogalma nem tartalmazná a folytonosságot, akkor a függvény fogalmának ez a nemlétező általánosítása Descartes-szorzatról fibrált nyalábra ennyi lenne: Egy H bázisterű, E teljes terű és Π projekciójú fibrált nyaláb (globális) szelése E-nek egy olyan Gs részhalmaza, hogy H tetszőleges x eleméhez pontosan egy olyan e eleme van Gs -nek, hogy Π(e) = x. Nevezzük ezt a hiányosan definiált definiált szelést mondjuk pszeudo-szelésnek (akár kiscicának is nevezhetnénk, mert csak a szelés valódi definíciójának kimondásához van rá szükségünk)
Nézzük akkor a folytonosságot!
Függvények esetén folytonosságról akkor van értelme beszélni, ha H és K topologikus terek, vagyis értelmezve van bennük a nyílt halmaz fogalma. Egy f: H → K függvény definíció szerint folytonos, ha K tetszőleges N nyílt halmazának ősképe, vagyis a proj1(Gf ∩ H × N) halmaz nyílt halmaz H-ban.
Ezt már tovább tudjuk vinni a szelésre is: a globális szelés olyan pszeudo-szelés, amelyben E tetszőleges M nyílt halmazának ősképe, vagyis a Π(Gs ∩ M) halmaz nyílt halmaz H-ban.
A lokális szelés ugyanez H helyett annak tetszőleges U nyílt részhalmazával elmondva.
Megjegyzések
A matematikai élő nyelvben általában sem a függvénynek, sem a szelésnek nem ezt a halmazos megfogalmazását használják. Nem Gf-ről és Gs-ről, hanem inkább f(x)-ről és s(x)-ről beszélnek. A két beszédmód közti kapcsolat: f(x) az {y| (x',y) ∈ Gf , proj 1 ( x',y ) = x } egyelemű halmaznak, s(x) pedig az {e| e ∈ Gs , Π(e) = x} egyelemű halmaznak az egyetlen elemét jelenti. Gf-et és Gs-t a függvény grafikonjának, illetve a szelés értékkészletének szokás nevezni. A későbbiekben adott s szelés esetén s(x) -et mi is az itt mondott értelemben fogjuk használni. Ekkor tehát az általános szokásnak megfelelően s-t egy olyan folytonos H → E függvénynek tekintjük, amelyre Π(s(x)) = x.
- A vektornyalábok szeléseit vektormezőknek nevezik. A fentiek alapján látható, hogy ez nem azonos a vektor értékű függvény fogalmával, bár ugyanúgy hasonlít rá, mint ahogy egy fibrált nyaláb hasonlít egy Descatres-szorzathoz.
- Az 1. (A téridő mint fibrált nyaláb) bejegyzésben definiált newtoni téridőnek, mint fibrált nyalábnak a szelései a pontszerű részecskékék világvonalai.