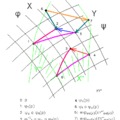
Az előző bejegyzésben szereplő sebességmező, vagyis egy forgó merev test adott pillanatbeli sebességmezeje egy Killing vektormező. Persze a Killing vektormezőnek nem ez a definíciója. Azt általában a Riemann-terek izometrikus folyamainak a sebességmezejeként szokás emlegetni, de még általánosabb értelemben tetszőleges sokaságon adott automorfizmus-csoport tetszőleges egyparaméteres részcsoportjának a hatása által generált folyam sebességmezejeként. A forgó merev testünk esetén ez a csoport az SO(3) csoport, az egyparaméteres részcsoport pedig egy olyan SO(3)-beli görbe, amely egyenletes forgást ír le. Persze az egyparaméteres részcsoportot sem így szokás definiálni, hanem úgy, hogy egy topologikus csoportban haladó olyan g görbe, amelyre g(t+s)=g(t)g(s), vagyis az olyan görbék, amik a valós számok additív csoportjának nemcsak homeomorf (oda-vissza folytonos és kölcsönösen egyértelmű), hanem homomorf (művelettartó) leképezése is (pontosabban szólva, a homeomorfizmust csak az egységelemnek valamely környezetében várjuk el). Az, hogy SO(3) egy egyparaméteres részcsoportja tényleg egyenletes forgást ír le, onnan látszik, hogy egy kiszemelt r pont helye a t = 0 pillanatban g(0)r = r, sebessége
v(r,0) = (d/dt) |t=0g(t)r = limt→0(g(t)r-r)/t .
Egy 0-hoz elég közeli s pillanatban az r pontban az r' = g-1(s)r pont van, a sebessége pedig
v(r,s) = limt→0(g(s +t)r'-r)/t = limt→0(g(t)g(s)r'-r)/t = limt→0(g(t)r-r)/t = v(r,0)
Az r pontbeli sebesség tehát tetszőleges pillanatban megegyezik a 0 pillanatbelivel. A fenti egyenlőség-láncban a második az, ami az egyparaméteres részcsoportokra kirótt g(t+s)=g(t)g(s) feltétel következménye.
Az előző bejegyzés tanulsága szerint a Killing vektormezők kölcsönösen egyértelmű kapcsolatban vannak a Lie-algebra vektoraival: a Lie-algebra (vagyis TeG) tetszőleges x eleme meghatároz a G csoporton egy jobb (bal-) invariáns vektormezőt: ez azokból a vektorokból áll, amelyekhez a Maurer-Cartan forma x-et rendeli. Ennek a G csoporton adott vektormezőnek a csoporthatás érintőleképezése általi képe az illető x elemhez tartozó Killing vektormező.