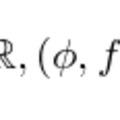Newton törvényeitől a Higgs-bozonig

Megszoktuk, hogy tetszőleges adott H és K topologikus terek esetén definiálható H-ból K-ba ható folytonos függvény. Például K-nak tetszőleges k elemét kiszemelve a f: H → K : x → k függvény ilyen. A halmazos megfogalmazásunkkal ez a függvény a G_f = {(x, k) | x ∈H } halmaz.

Az azonban már nem igaz, hogy tetszőleges H bázisterű, K fibrumú és E teljes terű fibrált nyalábnak lenne globális szelése.

Erre mutatok most egy példát.

Legyen H = {z | z ∈ C , |z|=1 }, vagyis egy egységsugarú kör a komplex számsíkon a szokásos topológiával, K = {-1,1} és E = H .

 Legyen a  Π projekció az E → H : z → z² leképezés. Ennek a nyalábnak nincs globális szelése! Indirekt módon tegyük fel ugyanis, hogy van. Ekkor

1. Létezik olyan G_s ⊆ E halmaz, hogy minden z ∈ H elemhez pontosan egy olyan e ∈G_s elem van, hogy Π(e) = z,
2. Tetszőleges M ⊆ E nyílt halmazra Π(G_s ∩ M) halmaz nyílt halmaz H-ban.

Tekintsük H-nak a H₀ = { e^iφ | 0 < φ < 2π} nyílt részhalmazát, vagyis az  eⁱ⁰ = 1 komplex szám kivételével az egész kört.

Legyen M₁ = { e^iφ | 0 < φ < π} és M₂ = { e^iφ | π < φ < 2π} E két nyílt részhalmaza.

 Az indirekt feltevésünk 2. pontja szerint Π(G_s ∩ M₁ ) is és Π(G_s ∩ M₂ ) is nyílt halmaz H-ban. Mivel a  Π leképezésünk is folytonos, ez azt jelenti, hogy G_s ∩ M₁ és G_s ∩ M₂ halmazok, mint egy nyílt halmaz folytonos leképezés általi ősképei, maguk is nyílt halmazok.  

Másrészt a feltevésünk 1. pontja szerint Π(G_s ∩ M₁ )  ∩  Π(G_s ∩ M₂ )  = Ø és Π(G_s ∩ M₁ )  ∪  Π(G_s ∩ M₂ )  = H₀ , vagyis  Π(G_s ∩ M₁ ) és  Π(G_s ∩ M₂) egymásnak H₀-ra vonatkozó komplementerei, vagyis mindkettő zárt is. Lévén, hogy H₀ összefüggő, H₀ részhalmazai közül csak az üres halmazra és a teljes H₀-ra áll fenn, hogy nyílt is és zárt is. Ezért, és mert  Π(G_s ∩ M₁ ) és  Π(G_s ∩ M₁ ) egymásnak H₀-ra vonatkozó komplementerei, az egyikük üres, a másikuk H₀. A határozottság kedvéért tegyük fel, hogy Π(G_s ∩ M₂) üres (a másik eset ugyanígy tárgyalható). Ekkor Π(G_s ∩ M₁ ) = H₀ és G_s ∩ M₂= Ø.

A kérdés már csak a H \ H = {1} halmaz egyetlen eleméhez G_s-nek melyik eleme tartozik, vagyis, G_s-nek melyik az az e₀ eleme, amelyre Π(e₀) = 1.

Erre két lehetőség van: vagy e₀ = 1 (= eⁱ⁰), vagy e₀ = -1 (= e^iπ).

 Ha e₀ = 1, akkor az M = { e^iφ | -1 < φ < 1} nyílt halmazzal  Π(G_s ∩ M) = Π((G_s ∩ M ∩ M₁)∪{eⁱ⁰}) = Π({ e^iφ | 0 ≤ φ < 1})  = { e^2iφ | 0 ≤ φ < 1},  ha e₀ = -1 akkor pedig az M = { e^iφ | π-1 < φ < π+1} nyílt halmazt véve  Π(G_s ∩ M) = Π((G_s ∩ M ∩ M₁)∪{e^iπ}) = Π({ e^iφ | π-1  < φ  ≤ π })  = { e^2iφ | π-1  < φ  ≤ π }. Mivel ezek a halmazok nem nyíltak, az indirekt feltevésünkkel ellentmondásra jutottunk. Tehát ennek a nyalábnak nincs globális szelése!